Законы алгебры высказываний

Одно из важных изобретений человека, которое легло в основу алгебры, - это введение буквенной символики для записи свойств операций. К примеру, тот же переместительный закон сложения записывается с помощью букв совсем просто a+b=b+a. Такие равенства, которые верны при любых значениях букв, называются, как вы помните, тождествами. По мере изучения алгебры тождеств появлялось все больше и больше. Достоинством тождеств является то, что, подставляя одни тождества в другие, можно получать новые тождества. Такую процедуру называют тождественным преобразованием.

Существует алгебра высказываний - раздел математической логики, изучающий свойства операций над высказываниями. Прежде всего нас будут интересовать те свойства, которые записываются как тождество. В нашем случае буквы будут обозначать произвольные высказывания, а знак равенства будет по-прежнему выражать тот факт, что значение левой части равенства совпадает со значением правой части равенства, какие бы высказывания мы в них ни подставили. В математической логике такие тождественно равные высказывания принято называть равносильными. Сами высказывания, в которых фигурируют буквы, обозначающие произвольные высказывания и соединенные знаками логических операций, называют формулами. Буквы, входящие в такие формулы, называют логическими переменными. Формулы называют тождественно равными или равносильными, если равносильны представленными ими высказывания.

В алгебре действительных чисел доказательство тождеств подчас является довольно трудным делом, требующим определенной изобретательности. В алгебре высказываний доказательство тождества - процесс несложный, хотя и может оказаться весьма трудоемким.

Приведем список основных тождеств алгебры высказываний.

Приведенные выше законы алгебры логики обычно используют для преобразования одних формул в другие, им равносильные.

Вот пример:

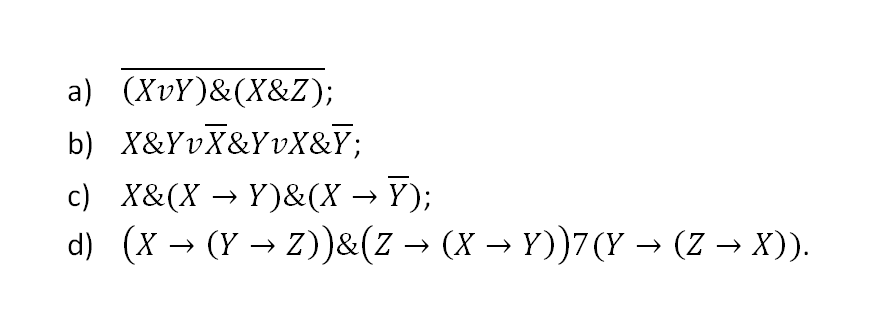Первое равенство в этой цепочки объясняется применением формулы 21, второе и третье равенства имеют место согласно законом де Моргана, чнтвертое получается применением формулы двойного отрицания, пятое равенство - это последовательное применение законов коммутативности и дистрибутивности, шестое равенство имеет место в силу формулы 14, седьмое - в силу формулы 11, восьмое - это опять применение дистрибутивного закона, девятое равенство верно в силу формулы 13 и, наконец, десятое равенство объясняется формулой 12.

Формула называется тождественно истинной или тавтологией, если она принимает значение Истина при любых значениях входящих в нее переменных. Примером простейшей тавтологии является формула X->X.

Математическая логика лишь моделирует логику человеческого рассуждения. К примеру, высказывания X & Y и Y & X математическая логика признает равносильными. И действительно, высказывания "Идет дождь, и дует ветер" и "Дует ветер, и идет дождь" в смысловом содержании идентичны друг другу. Но сравните высказывания "Она вошла в зал, и заиграла музыка" и "Заиграла музыка, и она вошла в зал", и вы чувствуете тонкую, но вполне уловимую разницу, идущую от человеческого восприятия союза "и" как некой упорядоченности событий по времени.

Вопросы и задания!

1. Какие высказывания, содержащие переменные, обозначающие высказывания, называются равносильными?

2. Проверьте законы де Моргана, составив соответствующие таблицы истинности.

3. Проверьте, что следующие формулы являются тавтологиями:

а) X -> X; б) X -> (Y -> X).

4. Упростите следующие формулы:

Назад В начало Далее

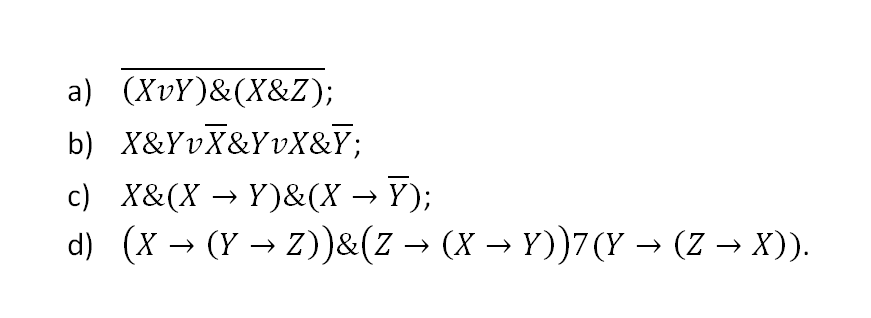Календарь

Калькулятор

Поиск

Друзья сайта

Дискретная математика

Законы алгебры высказываний